Tag: Effect

Supersolids are a fundamental phase of matter originated by the spontaneous breaking of the gauge symmetry as in superfluids and superconductors and of the translational symmetry as in crystals^13,14,15,16. This gives rise to a macroscopic wavefunction with spatially periodic modulation and to mixed superfluid and crystalline properties. Supersolids were originally predicted in the context of solid helium^13,14,15,16. Today, quantum phases with spontaneous modulation of the wavefunction are under study in a variety of bosonic and fermionic systems. These include: the second layer of ⁴He on graphite^1,2; ultracold quantum gases in optical cavities⁵, with spin–orbit coupling⁶ or with strong dipolar interactions^7,8,9,21; the pair-density-wave phase of ³He under confinement^3,4; and pair-density-wave phases in various types of superconductor^10,11,12. Related phases have been observed in frustrated magnetic systems²² or proposed to exist in the crust of neutron stars²³ and for excitons in semiconductor heterostructures²⁴. The periodic structure of the wavefunction of all these systems is a prerequisite for supersolidity, which has so far, however, emerged clearly only in some cold-atom systems with the evidence of the double spontaneous symmetry breaking and of the mixed superfluid-crystalline character^5,25,26. The experiments carried out so far on the other types of system have proved the coexistence of superfluidity/superconductivity and crystal-like structure^{1,2,3,4,10,11,12}, but no quantitative connection of the observations to the concept of supersolidity has been made. One of the difficulties in comparing different types of system with spatial modulation of the wavefunction is the seeming lack of a universal property quantifying the deviations from the dynamical behaviour of ordinary superfluids or superconductors.

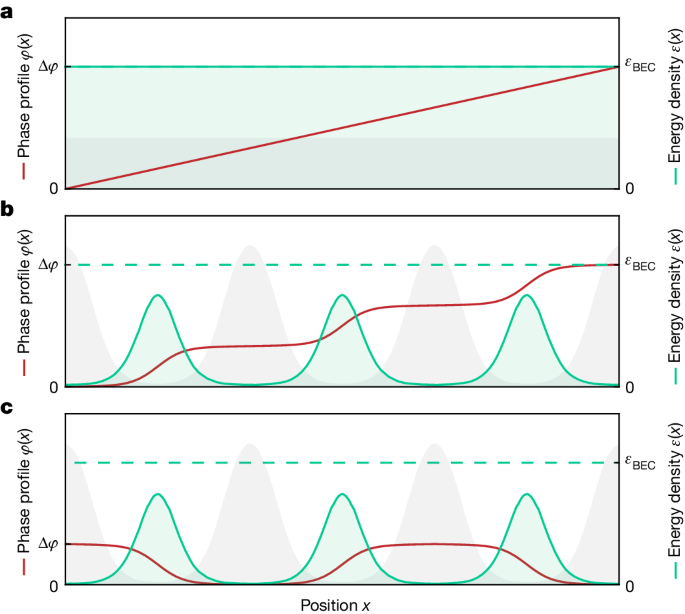
Here we note that a property with such characteristics already exists, the so-called superfluid fraction of supersolids, well known in the field of superfluids but not in that of superconductors. The superfluid fraction, introduced by A. J. Leggett in 1970 (ref. ¹⁶), quantifies the effect of the spatial modulation on the superfluid stiffness, which is in itself a defining property of superfluids and superconductors. The superfluid stiffness indeed measures the finite energy cost of twisting the phase of the macroscopic wavefunction and accounts for all fundamental phenomena of superfluidity, such as phase coherence, quantized vortices and supercurrents²⁷. As sketched in Fig. 1, whereas in a homogeneous superfluid/superconductor the phase varies linearly in space, in a modulated system, most of the phase variation can be accommodated in the minima of the density, reducing the energy cost. Because the superfluid velocity is the gradient of the phase, this implies that peaks and valleys should move differently, giving rise to complex dynamics with mixed classical (crystalline) and quantum (superfluid) character. For example, fundamental superfluid phenomena such as vortices and supercurrents are predicted to be profoundly affected by the presence of the spatial modulation, losing the canonical quantization of their angular momentum^16,17,18,28. The superfluid fraction, which ranges from unity for standard superfluids to zero for standard crystals, enters directly in all these phenomena and is therefore the proper quantity to assess the deviations from standard superfluids and superconductors. Note that the superfluid fraction of supersolids is not related to thermal effects, in contrast to the superfluid fraction owing to the thermal depletion of superfluids and superconductors²⁹.

Sketches of the superfluid fraction from the application of a phase twist in a bosonic system at zero temperature. a, In a homogeneous superfluid, a phase twist with amplitude Δφ results in a constant gradient of the phase, that is, a constant velocity, whereas in a supersolid (b,c), the kinetic energy can be minimized by accumulating most of the phase variation in the low-density regions. The grey and green areas represent the number density and the kinetic energy density, respectively, whereas the phase profile is plotted in red. The superfluid fraction is the ratio of the area under the green curve to that of the homogeneous case. b, Leggett’s approach, which—for an annular system—would correspond to a stationary rotation, leads to a monotonous increase of the phase. c, Our method, based on an alternating oscillation of the phase, leads to Josephson oscillations. Both kinetic energy and superfluid fraction are the same for b and c.

The standard methods to measure the superfluid stiffness are based on the measurement of global properties such as the moment of inertia for rotating superfluids^1,2 or the penetration depth of the magnetic field for superconductors³⁰. In dipolar supersolids, previous attempts using rotational techniques revealed a large superfluid fraction³¹ but were not precise enough to assess its sub-unity value^32,33. In the other systems, there is evidence that the superfluid stiffness is low^1,2,30, but no quantitative measurement of a sub-unity superfluid fraction is available.

In this work, we demonstrate that it is possible to measure the superfluid fraction of a supersolid not only from global dynamics but also from a fundamental phenomenon taking place in individual cells of the supersolid lattice: the Josephson effect¹⁹. As sketched in Fig. 1, the unit cell of a 1D supersolid lattice is composed by two density maxima connecting through a density minimum, so it has the typical structure of a Josephson junction, two bulk superfluids connected by a weak link. It is therefore tempting to associate supersolidity to the very existence of local Josephson dynamics. So far, the analogy between a supersolid and an array of Josephson junctions has only been used to model the relaxation towards the ground state of a dipolar supersolid²⁰. There is instead no theoretical or experimental evidence for local Josephson oscillations or an understanding of the potential relation between the Josephson effect and the superfluid fraction. The problem is complicated by the fact that, in supersolids, the weak links are self-induced by internal interactions rather than by an external potential, so they can change during the dynamics. Therefore, it is not clear if phenomena such as Josephson oscillations can exist at all in a supersolid.

Here we demonstrate experimentally and theoretically that a supersolid can, in fact, sustain coherent phase-density oscillations, behaving as an array of Josephson junctions. We also show that the Josephson coupling energy that we can deduct from the Josephson oscillations provides a direct measurement of the superfluid fraction. We use this new approach to measure with high precision the superfluid fraction of the dipolar supersolid appearing in a quantum gas of magnetic atoms. We find a range of sub-unity values of the superfluid fraction, depending on the depth of the density modulation in accordance with Leggett’s predictions.

Leggett’s approach to the superfluid fraction considers an annular supersolid in the rotating frame and maps it to a linear system with an overall phase twist, as sketched in Fig. 1b. The superfluid fraction is defined on a unit cell as^16,34

The numerator is the kinetic energy acquired by the supersolid with number density n(x) when applying a phase twist Δφ over a lattice cell of length d, \({E}_{{\rm{kin}}}={\hbar }^{2}/(2m){\int }_{{\rm{cell}}}dx\,n(x)\,{| \nabla \varphi (x)| }^{2}\), and thus accounts for density and phase modulations. The denominator \({E}_{{\rm{kin}}}^{{\rm{\hom }}}=Nm{v}_{{\rm{s}}}^{2}/2\) is the kinetic energy of a homogeneous superfluid of N atoms and velocity v_s = ħΔφ/(md) associated with a constant phase gradient Δφ across the cell. Using a variational approach^16,35, Leggett found an upper and a lower bound for equation (1), \({{f}_{{\rm{s}}}}^{{\rm{l}}}\le {f}_{{\rm{s}}}\le {{f}_{{\rm{s}}}}^{{\rm{u}}}\); see Methods. In particular, the upper bound

in which \(\bar{n}(x)\) is the normalized 1D density, restricts f_s to be lower than unity if the density is spatially modulated. Note that the calculation of the superfluid fraction, which is a global property, by considering a single lattice cell is possible owing to the periodicity of the wavefunction of the supersolid¹⁶.

We propose an alternative expression for the superfluid fraction, considering Josephson phase twists with alternating sign between neighbouring lattice sites of a supersolid, as sketched in Fig. 1c. This corresponds to a different type of motion of the supersolid, with no global flow but with alternate Josephson phase-density oscillations between sites. Also, in this case, we can consider a single cell, because the kinetic energy is proportional to |∇φ(x)|², so it does not depend on the sign of the phase twist. In the limit of small excitations (Δφ → 0), the kinetic energy of a Josephson junction is given by E_kin = NKΔφ², in which K is the coupling energy across the barrier³⁶. From equation (1), we thus find:

showing a direct relation between the superfluid fraction and the coupling energy of the junction. We note that an expression similar to the upper bound in equation (2) was derived by Leggett for the coupling energy of a single Josephson junction³⁷, however without discussing the connection to the superfluid fraction.

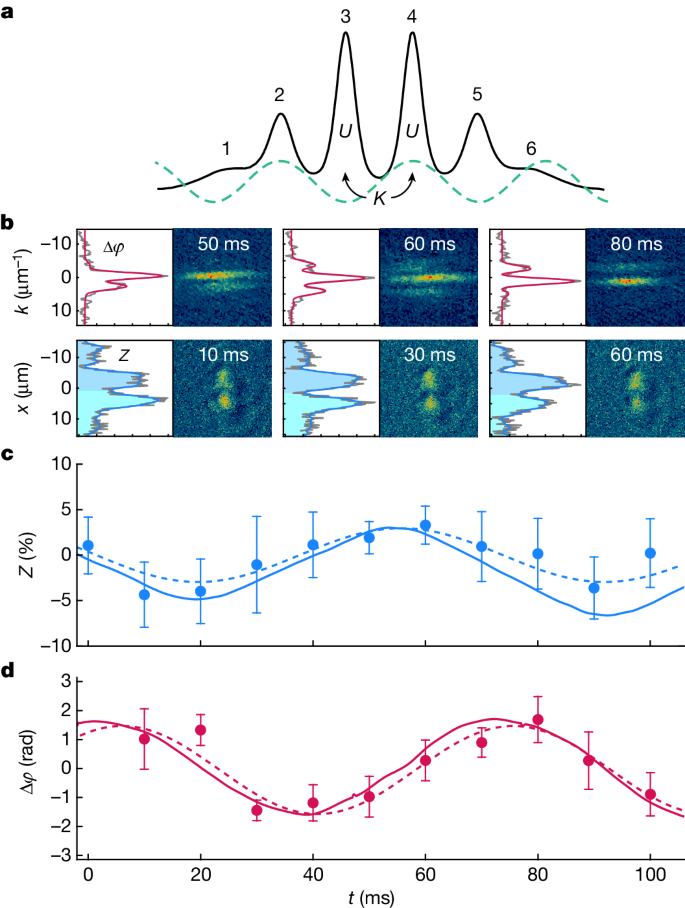
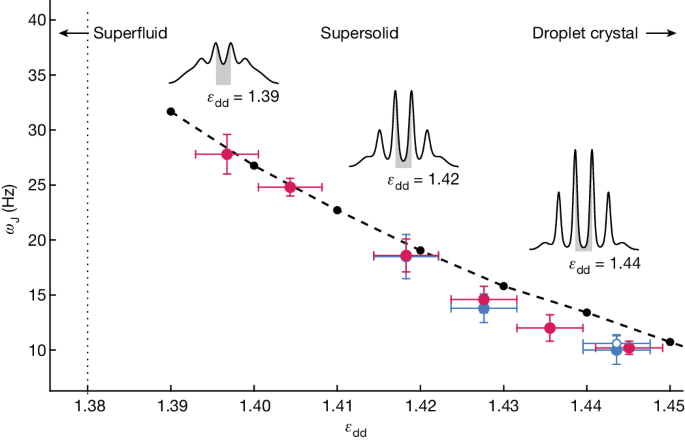
We now demonstrate the existence of coherent Josephson-like oscillations in a dipolar supersolid^7,8,9. This system is particularly appealing to study fundamental aspects of supersolidity³⁸: the supersolid lattice is macroscopic, with many atoms per site and large superfluid effects; the available control of the quantum phase transition allows to directly compare supersolids and superfluids; and interactions are weak, allowing a fairly accurate theoretical modelling³⁹. Our experimental system⁷ is composed of about N = 3 × 10⁴ bosonic dysprosium atoms, held in a harmonic trap elongated along the x direction, with trap frequencies (ω_x, ω_y, ω_z) = 2π(18, 97, 102) Hz. By tuning the relative strength ε_dd of dipolar and contact interactions, we can cross the quantum phase transition from a standard Bose–Einstein condensate (BEC) to the supersolid regime (Methods). The supersolid lattice structure is 1D, leading to a continuous phase transition⁴⁰. Our typical supersolid is made of two main central clusters and four smaller lateral ones, with a lattice period d ≃ 4 μm, as shown in Fig. 2. We can vary the density modulation depth by varying the interaction strength in the range ε_dd = 1.38–1.45; further increasing ε_dd leads to the formation of an incoherent crystal of separate clusters, the so-called droplet crystal, a regime that we cannot study experimentally because of its short lifetime⁷.

a, Sketch of the experimental system. The black line is the supersolid density profile at equilibrium. The dashed green line is the optical lattice potential used for the phase imprinting. b, Examples of experimental single shots and corresponding integrated 1D profiles. Top row, interference fringes after a free expansion. Red curves are fit functions used to extract the phase difference Δφ. Bottom row, in situ images. Shaded areas indicate the populations of the left and right halves of the supersolid used to extract the population imbalance Z. c, Oscillations of Z as a function of time at ε_dd = 1.428. Dots are experimental points. Error bars are the s.e.m. of 20–30 measurements. The solid line is the numerical simulation for the same parameters. The dashed line is a sinusoidal fit to the experimental data. d, Same for Δφ. Experimental values and error bars are calculated using the circular mean and s.e.m. (see Methods).

Source Data

Because our system is inhomogeneous, we focus our attention on the central cell, the one delimited by clusters 3 and 4 in Fig. 2. As we will show, the superfluid fraction we derive from that cell corresponds to the superfluid fraction of a hypothetical homogeneous supersolid with all cells identical to the central cell, as in Fig. 1, which is the system of general interest.

We find that the application for a short time of an optical lattice with twice the spacing of the supersolid (sketched in Fig. 2a) imprints the proper alternating phase difference between adjacent clusters to excite Josephson oscillations. With a depth of 100 nK and an application time of τ = 100 μs, we obtain a phase difference on the order of π/2. After a variable evolution time in the absence of the lattice, we measure both the evolving phase difference Δφ between neighbouring clusters and the population difference Z between the left and right halves of the supersolid. Δφ is measured from the interference fringes developing after a free expansion (snapshots in Fig. 2b, top row), whereas Z is measured by in situ phase-contrast imaging (Fig. 2b, bottom row) (Methods). As shown in Fig. 2c,d, we observe single-frequency oscillations of Z and Δφ, with the characteristic π/2 phase shift of the standard Josephson dynamics^{19,36,41,42,43,44}. The observation time is limited to about 100 ms by the finite lifetime of the supersolid, owing to unavoidable particle losses⁷. The experimental observations agree very well with numerical simulations based on the time-dependent extended Gross–Pitaevskii equation (GPE), also shown in Fig. 2c,d (Methods). We have checked that the Josephson oscillations are not observable if we apply the same procedure to standard BECs instead of supersolids (see Methods).

The observation of a single frequency in both experiment and simulations indicates that not only is it possible to excite Josephson-like oscillations in a supersolid but also they are a normal mode of the system. To model our observations, we develop a six-mode model, generalizing the two-mode Josephson oscillations³⁶ to the case of six clusters (see Methods). We associate to the jth cluster a population N_j and a phase φ_j (j = 1,…,6). In general, the dynamics includes contributions from each cluster and shows several frequencies. However, we find that, under appropriate conditions among the interaction and coupling energies, there exists a normal mode of the system in which the dynamical variables of the two central clusters of the supersolid decouple from the lateral ones. This results in Josephson-like oscillations described by the two coupled equations

in which ΔN = N₃ − N₄, N₃₄ = N₃(0) + N₄(0), Δφ = φ₃ − φ₄ and U is the interaction energy per particle. These equations hold for interaction energies N₃₄U much larger than K (for our system, N₃₄U/(2K) > 25; see Methods). Because in our case ΔN ≪ N, we keep only linear terms in ΔN/N.

Equations (4a) and (4b) are equivalent to those of a simple pendulum with angle Δφ and angular momentum ΔN and, in the small-angle limit, feature sinusoidal oscillations with a single frequency, \({\omega }_{{\rm{J}}}=\sqrt{4{KUN}_{34}}\). We emphasize that the current–phase relation equation (4a) as well as ω_J² differ by a factor of 2 with respect to the Josephson equations of two weakly coupled BECs, owing to the contribution of the lateral clusters, but are equal to those of a hypothetical homogeneous supersolid. Notice also that equations (4a) and (4b) depend only on the coupling energy K and the interaction energy U of the two central clusters, in contrast to the expectation that the inhomogeneity of the trapped system may introduce other energies in the equations of motion. We checked by Gross–Pitaevskii simulations that our experimental configuration satisfies the conditions to have a Josephson-like normal mode (namely, equation (7) in Methods).

In the experiment, we are not able to resolve the population of the individual clusters but we study the population difference between the left and right halves of the system, Z = (N₁ + N₂ + N₃ − N₄ − N₅ − N₆)/N. There is a proportionality relation between the two observables, ΔN = 2NZ, which allows us to rewrite equations (4a) and (4b) in terms of the experimental observables (Methods).

An important difference between a cell of the supersolid and a standard Josephson junction is the fact that, in the supersolid, the position of the weak link is not fixed by an external barrier but it is self-induced, so it can move. This leads to the appearance of a low-energy Goldstone mode associated with the spontaneous translational symmetry breaking. In a harmonic potential, it consists of a slow oscillation of the position of the weak link, together with the density maxima, and an associated oscillation of both Z and Δφ (ref. ²⁶). Owing to its low frequency (on the order of a few Hz), the Goldstone mode is spontaneously excited by thermal fluctuations, resulting in shot-to-shot fluctuations of the experimental observables. The same low frequency, however, allows to separate Josephson and Goldstone dynamics in both experiment and theory (Methods).

We measure the Josephson frequency ω_J from a sinusoidal fit of the phase and population dynamics in Fig. 2c,d. We repeat the measurement by varying the interaction parameter ε_dd, corresponding to different depths of the supersolid density modulation. Figure 3 shows the fitted frequencies as a function of ε_dd and a comparison with the numerical simulations. We observe a decrease of the frequency for increasing ε_dd. This is justified by the fact that the superfluid current across the junction decreases because a larger and larger portion of the wavefunction remains localized inside the clusters (see insets in Fig. 3). This reduces the coupling energy K while only weakly affecting the interaction energy.

Red dots are the experimental frequencies for Δφ. Filled and open blue dots are the frequencies for Z measured by in situ imaging with and without optical separation, respectively (Methods). Vertical error bars are the uncertainties in the nonlinear fit of the sinusoidal oscillations shown in Fig. 2c,d. Horizontal error bars represent the experimental resolution in ε_dd (Methods). The red point at ε_dd = 1.444 is shifted slightly horizontally for clarity. Black points are the results of numerical simulations. The dashed line is a guide for the eye. The insets show the modulated ground-state density profiles obtained from numerical simulations for different values of ε_dd. The vertical dotted line marks the critical point of the superfluid–supersolid quantum phase transition.

Source Data

From the Josephson frequency, we can derive the coupling energy as K = ω_J²/(4UN₃₄), with the denominator obtained from the simulations. We verified that this relation holds not only in the small-amplitude regime of the simulations but also for the larger amplitudes of the experiment.

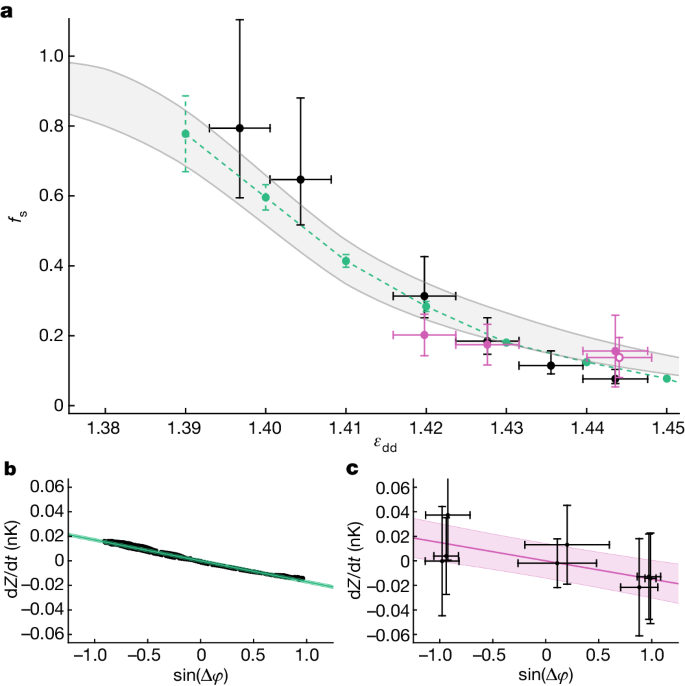
From the measured K, we derive in turn the superfluid fraction using equation (3). The results are shown in Fig. 4 and feature a progressive reduction of the superfluid fraction below unity for increasing depths of the supersolid modulation. The experimental data are in good agreement with the numerical simulations (green dots), in which—according to equation (4a)—the coupling energy is obtained from the linear dependence of dZ/dt on sin(Δφ) (current–phase relation); see Fig. 4b. A similar analysis (Fig. 4c) was performed on the experimental data for which we have combined phase and population oscillations (pink dots in Fig. 4a). The results for these data points demonstrate the reduced superfluid fraction of the supersolid with no numerical input on the interaction energy U.

a, Superfluid fraction as a function of ε_dd. Black dots are experimental results derived from the Josephson frequencies. Vertical error bars result from the error propagation of equation (3), with K = ω_J²/(4UN₃₄); see Methods. Green dots are results from numerical simulations. Error bars are the uncertainties of the linear fits used to determine K and UN₃₄. Pink points are derived from the experimental phase–current relation, as in c. Error bars are estimated using the propagation of equation (3), with K and its relative uncertainty extracted from linear fits of experimental data. The open pink point at ε_dd = 1.444 is the dataset without the optical-separation technique (Methods). The grey band extends between the upper and lower bounds of equation (1). b,c, Phase–current relation at ε_dd = 1.444. The points show the results of numerical simulations (b) and experimental measurements (c). From the linear regressions (green and pink lines), we extract the coupling energy K according to equation (4a). Shaded regions are the confidence bands for one s.d.

Source Data

In Fig. 4a, we also compare our results with Leggett’s prediction of equation (2), relating the superfluid fraction to the density modulation of the supersolid. From the numerical density profiles, we calculate both the upper bound \({{f}_{{\rm{s}}}}^{{\rm{u}}}\) and the corresponding lower bound³⁵ \({{f}_{{\rm{s}}}}^{{\rm{l}}}\), which delimit the grey area in Fig. 4a (see Methods). The two bounds would coincide if the density distribution were separable in the transverse coordinates y and z. Because our supersolid lattice is 1D, the two bounds are close to each other. The superfluid fraction calculated from the simulated dynamics lies between the two bounds in the whole supersolid region we investigated, demonstrating the applicability of Leggett’s result to our system.

In conclusion, the overall agreement between experiment, simulations and theory on our dipolar supersolid proves the long-sought sub-unity superfluid fraction of supersolids and its relation to the spatial modulation of the superfluid density. The demonstration of self-sustained Josephson oscillations in a supersolid provides a new proof of the extraordinary nature of supersolids compared with ordinary superfluids and crystals. These oscillations indeed cannot exist neither in crystals, in which particles are bound to lattice sites, nor in ordinary superfluids, which do not have a lattice structure.

Our findings open new research directions. The observed reduction of the superfluid fraction with increasing modulation depths may explain the low superfluid stiffness measured in other systems, such as ⁴He on graphite^1,2 or superconductors hosting pair-density-wave phases^10,11,12. An important question related to the pair-density waves in fermionic systems is how Leggett’s bounds on the superfluid fraction may be extended to systems in which the superfluid density and particle density do not coincide. Note that equation (2) is also applicable to standard superfluids with an externally imposed spatial modulation, as demonstrated for BECs in optical lattices by means of measurements of the effective mass⁴¹ or of the sound velocity^45,46. In the supersolid, however, the dynamics linked to the reduced superfluid fraction is not constrained by an external potential and so totally new phenomena might be observed. The large value of f_s we measured for the dipolar supersolid, which remains larger than 10% also for deep density modulations, indicates that partially quantized supercurrents^16,18 and vortices¹⁷ should appear at a macroscopic level.

Owing to the generality of the Josephson effect, our Josephson-oscillation technique might be applied to characterize the local superfluid dynamics of the other supersolid-like phases under study in superfluid and superconducting systems. Equation (3) is applicable in general, considering that the detection of Josephson oscillations implies measurement of both the coupling energy and the spatial period of the superfluid density modulation. For example, a promising type of system may be the pair-density-wave phase in superconductors, in which the modulation has already been resolved. The Josephson-oscillation technique works naturally in linear geometries and so it does not require any adaptation for the finite size of the clusters in the supersolid-like phases available in experiments^{1,2,3,4,5,6,7,8,9,10,11,12}, differently from the rotation technique¹⁶ (see Methods).

Furthermore, the self-induced Josephson junctions we have identified in supersolids might have extraordinary properties resulting from the mobility of the weak links. Indeed, although the Goldstone mode of the weak links is not relevant for the Josephson dynamics owing to its very low energy, for the same reason, it may affect the fluctuation properties of the junction⁴⁷, potentially leading to new thermometry methods⁴⁸ and especially to previously unknown entanglement properties⁴⁹.