[ad_1]
matemáticos ha sido descrito1 Una nueva clase de formas caracteriza las formas comunes en la naturaleza, desde las cámaras de la famosa concha espiral del nautilo hasta la forma en que se agregan las semillas en las plantas.
el un trabajo se considera matemáticas El concepto de “teselado”: cómo se forman las formas en una superficie. El problema de llenar un nivel con fichas idénticas ha sido explorado tan exhaustivamente desde la antigüedad que resulta tentador suponer que ya no queda nada por descubrir al respecto. Pero los investigadores extrapolaron los principios del mosaico con un nuevo conjunto de bloques geométricos con esquinas redondeadas, a los que llamaron “celdas lisas”.
“La geometría puede ser tan simple y, al mismo tiempo, tan profunda”: conozca a la ganadora del Premio de Matemáticas Claire Voisin
“En pocas palabras, nadie ha hecho esto antes”, dice Chaim Goodman-Strauss, matemático del Museo Nacional de Matemáticas de la ciudad de Nueva York, que no participó en el trabajo. “Es realmente sorprendente cuántas cosas fundamentales hay que hacer. considerar.”
Se sabe desde hace miles de años que sólo ciertos tipos de mosaicos poligonales, como cuadrados o hexágonos, pueden agruparse para llenar un espacio bidimensional sin espacios. Los mosaicos que llenan el espacio sin una disposición repetitiva regular, como los mosaicos de Penrose, han atraído interés desde el descubrimiento de estructuras no periódicas llamadas cuasicristales en la década de 1980. El año pasado, Goodman-Strauss y sus colegas informaron sobre la primera baldosa cuasi periódica, que carece de una verdadera periodicidad y utiliza sólo la forma de una única baldosa.2.
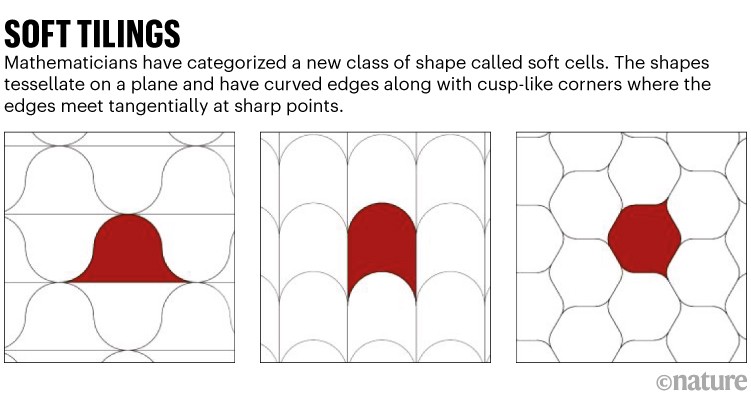
Fuente: Referencia 1
Evita las esquinas
El matemático Gabor Domokos de la Universidad de Tecnología y Economía de Budapest y sus colegas volvieron a las tejas poligonales periódicas, pero pensaron en lo que sucede cuando algunas de las esquinas son redondas. En dos dimensiones, no es posible redondear todas las esquinas sin dejar huecos. Pero los mosaicos que llenan el espacio se vuelven posibles cuando algunas de las esquinas se distorsionan en “formas de protuberancias”. Estos no tienen ángulos interiores: sus bordes se unen en forma de lágrima tangencial y encajan perfectamente junto a las esquinas redondeadas (consulte “Azulejos lisos”).
Domokos y sus colegas crearon un algoritmo para transformar suavemente mosaicos geométricos (ya sean polígonos 2D o poliedros 3D, como burbujas de espuma) en células suaves y exploraron la gama de formas posibles que permiten estas reglas. En 2D, las opciones son algo limitadas: todos los mosaicos deben tener al menos dos esquinas que parezcan protuberancias. Pero en 3D, la introducción de la suavidad depara algunas sorpresas. En particular, estas células lisas pueden llenar un espacio volumétrico sin tener esquinas.
Los investigadores crearon una medida cuantitativa del grado de “suavidad” de estos mosaicos 3D que llenan el espacio y descubrieron que los más suaves no son formas compactas, sino que desarrollan “alas” circulares en forma de crestas en sus bordes, que normalmente surgen de las superficies en forma de silla de montar de las baldosas. Los elementos de forma más suaves son en realidad discos circulares, a los que se acercan los bordes de los mosaicos 3D.
Costo del contrato
Domokos cree que en cualquier poliedro primario existe una pieza única que tiene la mayor suavidad posible. También sospecha que en materiales reales este óptimo resultaría en maximizar alguna cantidad física asociada, por ejemplo, con la energía de flexión en los bordes o la tensión superficial. Admite que ni él ni sus colegas tienen actualmente pruebas de esta conjetura sobre la máxima suavidad, pero espera que “alguien más inteligente adopte y demuestre esta conjetura”.
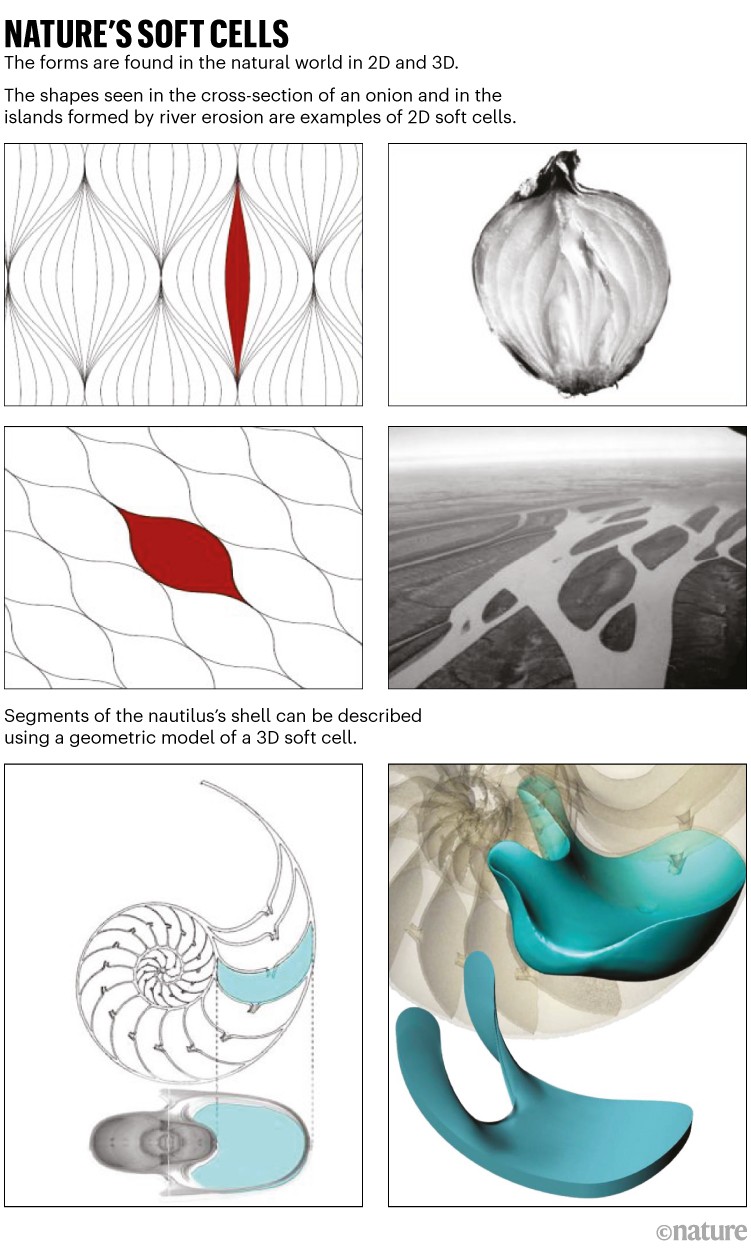
Fuente: Referencia 1
Los investigadores han identificado la presencia de tejas blandas en la naturaleza en las formas bidimensionales de las islas de los ríos trenzados, en las secciones transversales de capas concéntricas de las cebollas y en las células biológicas de los tejidos, así como en los compartimentos tridimensionales de conchas espirales como las encontrado en el nautilo, un molusco marino (ver 'Células blandas en la naturaleza'). Los investigadores creen que la naturaleza generalmente busca evitar las curvas, porque tales curvaturas tienen un alto costo en energía de deformación y pueden ser una fuente de debilidad estructural.
Domokos dice que el estudio del nautilo fue un “punto de inflexión” en el trabajo. En sección transversal, las cámaras de la corteza parecían células blandas bidimensionales con dos ángulos. Pero la coautora Kristina Rigoz, que también trabaja en la Universidad de Tecnología y Economía de Budapest, sospechaba que la sala 3D real no tenía ningún rincón. “Parecía increíble”, dice Domokos, “pero luego descubrimos que tenía razón”.
Geometría antigua
Dado que el análisis utiliza matemáticas conocidas desde hace siglos, puede parecer sorprendente que nadie haya formulado todavía el concepto de células blandas. Pero Goodman-Strauss sospecha que “los bordes blandos crean una barrera suficiente para la lisis de las células blandas”. ingenieros “Nunca antes había pensado en esto”.
“El mundo de los polígonos y poliedros es tan fascinante y rico que los matemáticos no necesitan ampliar su campo de juego”, afirma Domokos. Sospecha que existe una percepción común de que las nuevas ideas requieren matemáticas avanzadas o informática sofisticada, no sólo métodos de ingeniería establecidos.

El Centro Heydar Aliyev en Bakú fue diseñado por la arquitecta Zaha Hadid, cuyos edificios utilizan celdas lisas para evitar o minimizar las esquinas.Fotografía: Mladen Antonov/AFP vía Getty
Goodman-Strauss cree que este trabajo proporciona “una especie de lenguaje descriptivo de la estructura”, pero es posible que aún no revele nuevos principios físicos que subyacen a la formación de tales estructuras en la naturaleza. Para comprender las riberas de los ríos, por ejemplo, dice, probablemente aún será necesario considerar el proceso físico desde los primeros principios, como las funciones del flujo, el transporte de sedimentos y la erosión.
Domokos y sus colegas creen que arquitectos como Zaha Hadid han utilizado durante mucho tiempo células blandas de forma intuitiva para evitar o reducir esquinas, ya sea por razones estéticas o estructurales. Desde que completó la investigación, Domokos y el coautor Alan Gorrelli de la Universidad de Oxford, Reino Unido, han colaborado con arquitectos del California College of the Arts en San Francisco, quienes han creado una estructura galardonada utilizando elementos de células blandas fabricados – apropiadamente – de cáscaras de huevo.
[ad_2]
Source Article Link

